Through the years, Nature inspired computing [1] has been adapted by the computer science community to address challenging real-life problems. Biology-inspired and Physics-inspired processes have a huge influence on computer science, optimisation and machine learning. Darwin’s theory of natural evolution has inspired Genetic Algorithms.

In this blog, we focus on Genetic Algorithms and two of its applications in the domain of pattern recognition. In the sections that follow, we discuss fundamentals of genetic algorithms, pattern recognition, problem encoding, and two applications of genetic algorithms in the domain of pattern recognition, viz., optimal feature selection and optimal prototype selection.

Genetic Algorithms

Genetic algorithms(GAs) are part of a broad class of algorithms known as Evolutionary Algorithms. While there are a number of variants of GAs, in this blog, we discuss Simple Genetic Algorithm (SGA) to gain an appreciation of the fundamentals of this much broader subject.

GAs simultaneously explore a population of solutions. Starting with an initial population, which are parents belonging to the first iteration or first generation, they make use of genetic operators known as selection, crossover and mutation to arrive at the next generation or offsprings of fitter solutions. Through the Darwinian paradigm of survival of the fittest, the algorithm evolves solutions from one generation to another, culminating in arriving at a group of best solutions. It has theoretical guarantees through Schema Theory and Building Block Hypothesis [2,3] to achieve a global optimum. As the solutions evolve through generations, the search can be terminated through multiple criteria such as maximum number of iterations when there is no significant improvement in average fitness in success iterations or best fitness value, etc.

GAs have a number of applications not just limited to pattern recognition and optimisation. A critical aspect of GAs is the problem-encoding. We discuss two applications of GAs along with their contrasting problem-encoding in the domain of pattern recognition such as (a) Prototype Selection and (b) Feature Selection in the current blog.

To begin with, we discuss basic terminology of GAs below.

Chromosome: Each candidate solution is represented as a string of bits or chromosomes. Each chromosome has alleles which are binary valued. Figure-1 shows an example of one chromosome and its alleles. A population of solutions or equivalently population of chromosomes are initialised with 0’s and 1’s. The associated parameter is population size.

Figure 1. Chromosome of length 9 with allele values 0,1,1,0,1,0,0,1, and 1

Fitness function: It is the objective function of the optimisation problem, f(x). It provides a mechanism to evaluate each candidate solution or chromosome. An example of fitness function in case of pattern recognition is classification accuracy and in optimisation, it is the profit function (-ve of cost function) that we maximise.

Selection: From the population of offsprings, highly fit individuals are chosen to move to the next generation through multiple selection methods[4]. One popular selection method is proportionate selection, which ensures selecting a new population of chromosomes, proportionate to their fitness. Thus, more copies of highly fit individuals are chosen for the next generation.

Cross-over: Given two parent chromosomes, crossover operator helps to arrive at offsprings. There are multiple crossover mechanisms[5]. We discuss one of them known as ‘single point crossover’. It is carried out when a randomly generated probability is lower than the predefined Probability of Crossover at a randomly generated point of crossover. Figure-2 provides an example of crossover operation.The associated parameter is probability of crossover.

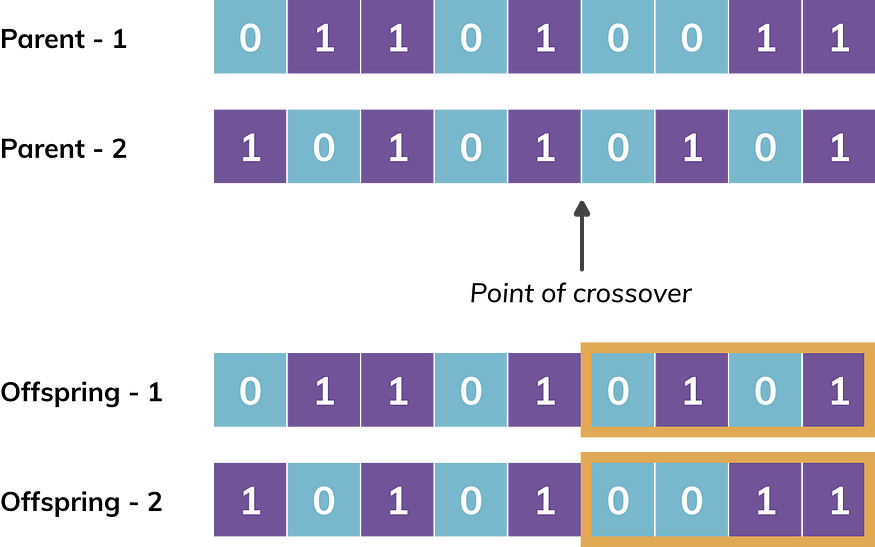
Figure-2. Crossover operation at a randomly generated point on two parent chromosomes resulting in two new offsprings. It may be noted that highlighted portions are exchanged between two parents to generate two offsprings.

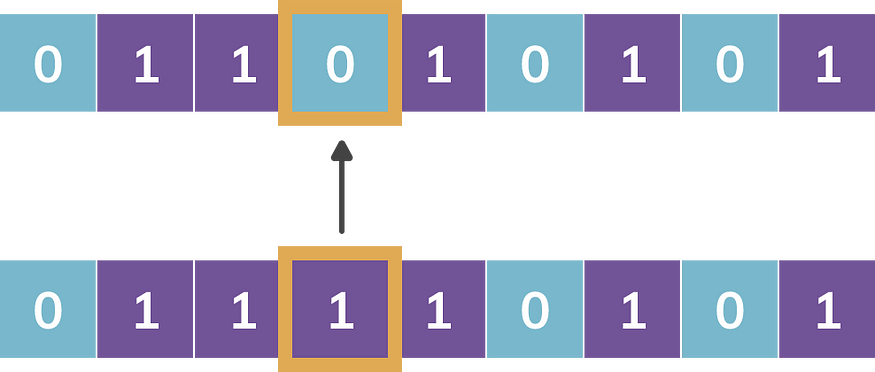
Mutation: Given a chromosome, when randomly generated probability is lower than the predefined Probability of Mutation, the allele (bit) value is flipped. It helps the solution to move out of local minimum and move towards global minimum. Figure-3 provides mutation operation. The associated parameter is probability of mutation.

**Figure 3**. Mutation operation is carried out at the randomly selected point. The figure contains before and after carrying out the mutation operation

Parameters of an SGA: In summary, the parameters of a simple genetic algorithm include population size or number of chromosomes, length of a chromosome, probability of crossover and probability of mutation. The choice of fitness function is important.

We provide a basic overview of pattern recognition and define the terms such as pattern, feature and objective of pattern recognition.

Pattern Recognition

A pattern is defined [6] as any thing opposite to chaos, it is an entity, vaguely defined, that could be given a name. Features are individual measurements of the attributes of a pattern. Some examples of patterns are (a) an image of a face, (b) handwritten digit, and ©computer monitor. And their corresponding features respectively are (a) each of the pixels or extracted-features like length of eyebrows, eye-width and length, nose length and width, lips length and width; (b) binary digits of presence or absence on predefined template; and (c ) dimensions of a monitor, reflectiveness, colour, bezel width, etc. The objective of pattern recognition is pattern classification. Thus, the features should help both pattern representation and discrimination.

We present two applications of genetic algorithms in pattern recognition known as optimal features selection and optimal prototype selection. We discuss each of them in detail in the later sections. We first discuss problem encoding in genetic algorithms, which is key to solving problems.

Problem Encoding in Genetic Algorithms

Each optimisation problem has its unique formulation in terms of the objective function and constraints. In the Genetic Algorithms paradigm, we optimise with respect to a fitness function. When we evaluate a chromosome through fitness function, we get fitness values. Through generations, we move to highly fit individuals or equivalently to better solutions. For the problems in the pattern recognition domain, some examples of the fitness functions are classification accuracy and metrics such as similarity metrics. The parameters are obtained through evolution from one generation through their encoded representation in the chromosomes. Each problem is encoded innovatively. In the following sections, we discuss two example encodings in relation to optimal feature selection and optimal prototype selection in the domain of Pattern Recognition.

Optimal Feature Selection

When a pattern is represented by too many features, the need for the number of patterns increases exponentially for effective pattern classification. And also, all the features may not help discrimination. It is difficult to choose important features manually. In view of this, the features could be selected such that the number of features is reduced and at the same time, high pattern classification accuracy is achieved, which is known as feature selection.

A discussion of feature selection approaches can be found in the work by G. Chandrasekhar and Ferat Sahin [7]

Genetic algorithms help us to select optimal subset of features while maximising classification accuracy.

Problem Encoding

Consider handwritten digit data. Each handwritten digit is represented as, say, 192 binary features. The digit can be visualised when arranged as a 16X12 matrix. Figure 1 contains a sample.

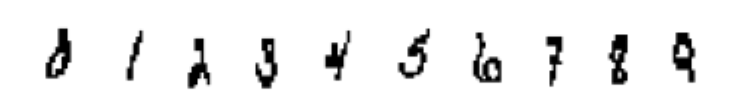
Figure 4: A sample of handwritten digit data

In this problem, the chromosome length is chosen as 192, fitness function is classification accuracy, probability of crossover is 0.95 and probability of mutation is 0.05. Through experiments [8], we achieved a reduction of the number of features from 192 to 93 while maintaining the same classification accuracy. It amounts to a reduction of features by 57%.

Optimal prototype Selection

Prototype selection refers to the selection of representative patterns from a large set of patterns. Once prototypes are obtained, an analysis that could be done on the entire data set could as well be done with a smaller set of prototypes without losing the abstraction or accuracy. This reduces the efforts needed for working on massive datasets, their storage and computation cost.

Some typical prototypes [9] from the data include patterns closest to centroids obtained through k-means in hyper-spherical data clusters, medoids [10] which are patterns identified through average minimal dissimilarity that are central to a set of patterns, and leaders [11] are the cluster representative patterns, that are identified based on a predefined distance threshold using leader clustering algorithm.

Problem encoding for leaders as prototypes

Consider handwritten digits having 10 classes, 0–9. The objective is to identify distance thresholds that provide an optimal set of prototypes. Each chromosome contains minimum and maximum distance or dissimilarity thresholds for each of 10 classes. For example, those limits for digit 0 are 2 and 7 and assume that they are in a similar range for each of the classes. If they represent about 6 bits per class, it amounts to 60 bits for 10 classes. Thus, the chromosome length is 60. The experiment results in selection of about 50% of prototypes through leaders from the given large dataset while providing best classification accuracy across other typical prototypes such as medoids and distance-based prototypes.

Summary

We discuss Genetic Algorithms which are used in a wide variety of problems in machine learning and optimisation. They are inspired by Darwin’s theory on survival of the fittest. Genetic algorithms are adapted when a solution through conventional optimization is difficult, or the search area consists of multiple local minima (maxima). The crossover operator ensures exploring fresh genetic material. The mutation helps avoid local minima. The selection method ensures that highly fit individuals are selected for the next generation. Thus, GAs help arriving at near-global optimal solutions. A population of near-optimal solutions are arrived at simultaneously.

We briefly provide an introduction to the concepts of pattern recognition and genetic algorithms. The main challenge in using GAs is the problem-encoding. We discuss two distinct ways of problem encoding while discussing the applications of GAs in optimal feature selection and optimal prototype selection.

A number of novel applications and extensions to genetic algorithms have happened over the years, including multi objective optimisation. We have discussed SGA in this blog to motivate the topic.

I would like to thank Trishna and Oshin for sparing their valuable time and effort in reviewing this article. And, thanks to Nikita Oliver for excellent artwork !