RAG pipelines have been an emerging technology, which leverage LLMs and vector DBs for indexing and retrieving content using conversational capabilities. Here we have talked about how you set up a RAG pipeline and make it operational. This blog deep dives into how to make semantic search more effective in a RAG pipeline.
In search, few of the use cases may completely work fine with semantic search, however, some of them may need something that delivers a better output. The problem with semantic search is, it can retrieve only the data it understands. It heavily depends on what context your chunk provides.
Language is inherently ambiguous. Misinterpreting the user’s intent, especially in complex queries where multiple meanings are possible is very common. A search for “Apple history” might return results about the company and the fruit, depending on how the semantic search interprets “Apple.” While semantic search excels in understanding natural language, it struggles to interact with structured data (like databases, product catalogs, or fact-based information).
Are there techniques that solve this better?
Hybrid search combines the powers of semantic search (contextual search) and keyword search (lexical search) and re-ranks them based on individual results. By leveraging traditional keyword search for precision and exact matches, and semantic search for understanding intent and context, hybrid models could address some of the outlined issues and provide better result sets.
Lexical Search: This is the traditional method that searches for keywords or exact text matches within documents. This is basically CMD+F on your chunks.
Semantic Search: This approach goes beyond the exact keyword matches and tries to understand the context and meaning behind search queries.
When does hybrid search become more than necessary?
For ‘out of domain’ data
Semantic Search only understands data on which your embedding model is trained on. Anything besides that is called ‘out of domain’ data. In these cases, combining with keyword search could be more beneficial.For tabular data
Hybrid search is particularly effective for querying files and data sources with a lot of tabular data. This includes files such as CSV, XLSX, and PDF with tables, as well as data sources like Notion and web pages.
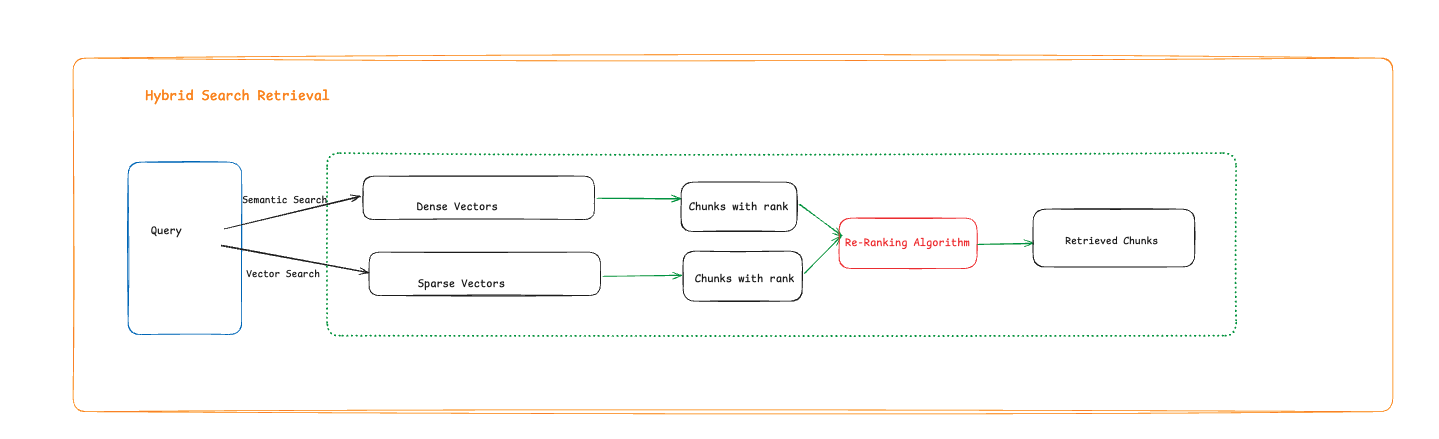
How does Hybrid Search work?
Hybrid search works on two different kinds of vectors:
i) Dense vectors for semantic searching
ii) Sparse vectors for keyword searching
There are two different queries: one for lexical search (exact match of words in the text) and the other for vector search (semantic match of words)
The answer gathered from both the results is re-ranked using re-ranking algorithms (e.g., Reciprocal Re-Ranking Algorithm)
And top N results are retrieved
What do sparse vectors even look like?
Consider your vocabulary contains only these words :
[“AI”, “intelligence”, “was”, “founded”, “discipline”, “1956”].
For the sentence “AI was founded as a discipline”, a sparse vector might look like this (assuming binary presence/absence for simplicity):
[“AI”, “intelligence”, “was”, “founded”, “discipline”, “1956”]
Sparse Vector: [1, 0, 1, 1, 1, 0]
Here:
1 indicates the presence of the word in the document.
0 indicates the absence of the word.
If using a TF-IDF weighting scheme, the values would reflect the importance of each term relative to the entire corpus, not just presence/absence.
What is TF–IDF weighting scheme?
In information retrieval, tf–idf (also TF*IDF, TFIDF, TF–IDF, or Tf–idf), short for term frequency–inverse document frequency, is a measure of importance of a word to a document in a collection or corpus, adjusted for the fact that some words appear more frequently in general.(source: Wikipedia)
1. Extended Vocabulary and Document Example
Let’s consider an extended vocabulary and a more complex document:
Vocabulary:
[“AI”, “intelligence”, “was”, “founded”, “discipline”, “1956”, “academic”, “field”, “research”, “study”, “machine”, “learning”]
Document:
“AI was founded as an academic discipline and a field of study.”
2. Term Frequency (TF) Calculation
The first step in constructing a TF-IDF weighted sparse vector is to calculate the Term Frequency (TF) for each word in the document. Term Frequency is the count of a term in the document, often normalized by the total number of terms in the document.
Document Term Count:
“AI”: 1
“was”: 1
“founded”: 1
“academic”: 1
“discipline”: 1
“field”: 1
“study”: 1
TF Calculation (assuming normalization by total terms):
Total number of terms in the document = 7
So,
TF(“AI”) = 1/7 ≈ 0.14
TF(“was”) = 1/7 ≈ 0.14
TF(“founded”) = 1/7 ≈ 0.14
TF(“academic”) = 1/7 ≈ 0.14
TF(“discipline”) = 1/7 ≈ 0.14
TF(“field”) = 1/7 ≈ 0.14
TF(“study”) = 1/7 ≈ 0.14
For all other terms in the vocabulary (e.g., “intelligence”, “1956”, “research”, “machine”, “learning”), TF = 0
3. Inverse Document Frequency (IDF) Calculation
IDF is a measure of how common or rare a term is across all documents in the corpus. The idea is to downweight terms that are common across many documents and up-weight those that are rare. IDF is calculated as:
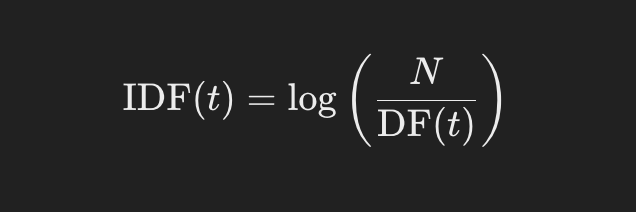
Assume the following DF (for simplicity):
“AI”: 1000 documents
“was”: 5000 documents
“founded”: 1200 documents
“academic”: 700 documents
“discipline”: 600 documents
“field”: 300 documents
“study”: 1500 documents
If the total number of documents
𝑁 =10,000
N=10,000, then:
IDF(“AI”) = log(10,000 / 1000) = log(10) ≈ 1
IDF(“was”) = log(10,000 / 5000) = log(2) ≈ 0.3
IDF(“founded”) = log(10,000 / 1200) ≈ 0.92
IDF(“academic”) = log(10,000 / 700) ≈ 1.15
IDF(“discipline”) = log(10,000 / 600) ≈ 1.22
IDF(“field”) = log(10,000 / 300) ≈ 1.52
IDF(“study”) = log(10,000 / 1500) ≈ 0.82
4. TF-IDF Weighted Sparse Vector
Now, we multiply the TF by the corresponding IDF for each term in the document to get the TF-IDF score for each term.
TF-IDF(“AI”) = 0.14 * 1 ≈ 0.14
TF-IDF(“was”) = 0.14 * 0.3 ≈ 0.042
TF-IDF(“founded”) = 0.14 * 0.92 ≈ 0.129
TF-IDF(“academic”) = 0.14 * 1.15 ≈ 0.161
TF-IDF(“discipline”) = 0.14 * 1.22 ≈ 0.171
TF-IDF(“field”) = 0.14 * 1.52 ≈ 0.213
TF-IDF(“study”) = 0.14 * 0.82 ≈ 0.115
5. Sparse Vector Representation
Given the vocabulary and TF-IDF calculations, the sparse vector for the document “AI was founded as an academic discipline and a field of study” would be represented as:
Vocabulary: [“AI”, “intelligence”, “was”, “founded”, “discipline”, “1956”, “academic”, “field”, “research”, “study”, “machine”, “learning”]
Sparse Vector:
[0.14, 0, 0.042, 0.129, 0.171, 0, 0.161, 0.213, 0, 0.115, 0, 0]
Code:
In the code below, we have used Milvus vector DB
Versions of Python: 3.12.3 , Pymilvus: 2.4.8
from milvus_model.hybrid import BGEM3EmbeddingFunction
from pymilvus import (
AnnSearchRequest,
Collection,
CollectionSchema,
DataType,
FieldSchema,
RRFRanker,
connections,
)
docs = [
"Artificial intelligence was founded as an academic discipline in 1956.",
"Alan Turing was the first person to conduct substantial research in AI.",
"Born in Maida Vale, London, Turing was raised in southern England.",
]
query = "Who started AI research?"
ef = BGEM3EmbeddingFunction()
dense_dim = ef.dim["dense"]
docs_embeddings = ef(docs)
query_embeddings = ef([query])
connections.connect("default", host="localhost", port="19530")
fields = [
# Use auto generated id as primary key
FieldSchema(name="pk", dtype=DataType.VARCHAR,
is_primary=True, auto_id=True, max_length=100),
FieldSchema(name="text", dtype=DataType.VARCHAR, max_length=512),
FieldSchema(name="sparse_vector", dtype=DataType.SPARSE_FLOAT_VECTOR),
FieldSchema(name="dense_vector", dtype=DataType.FLOAT_VECTOR,
dim=dense_dim),
]
schema = CollectionSchema(fields, "")
col = Collection("sparse_dense_demo1", schema)
sparse_index = {"index_type": "SPARSE_INVERTED_INDEX", "metric_type": "IP"}
dense_index = {"index_type": "FLAT", "metric_type": "COSINE"}
col.create_index("sparse_vector", sparse_index)
col.create_index("dense_vector", dense_index)
entities = [docs, docs_embeddings["sparse"], docs_embeddings["dense"]]
col.insert(entities)
col.flush()
col.load()
sparse_search_params = {"metric_type": "IP"}
sparse_req = AnnSearchRequest(query_embeddings["sparse"],
"sparse_vector", sparse_search_params, limit=2)
dense_search_params = {"metric_type": "COSINE"}
dense_req = AnnSearchRequest(query_embeddings["dense"],
"dense_vector", dense_search_params, limit=2)
result = col.hybrid_search([sparse_req, dense_req], rerank=RRFRanker(),
limit=2, output_fields=["text"])
print(result)
References:
https://cloud.google.com/vertex-ai/docs/vector-search/about-hybrid-search/



